En matemática, el teorema del binomio es una fórmula que
proporciona el desarrollo de la potencia n-ésima de n (siendo n, entero
positivo) de un binomio. De acuerdo con el teorema, es posible expandir la
potencia (x + y)n en una suma que implica términos de la forma axbyc, donde los
exponentes b y c son números naturales con b + c = n, y el coeficiente a de
cada término es un número entero positivo que depende de n y b. Cuando un
exponente es cero, la correspondiente potencia es usualmente omitida del
término.
lunes, 5 de noviembre de 2012
PRODUCTOS NOTABLES:
Productos notables es el nombre que reciben multiplicaciones
con expresiones algebraicas cuyo resultado se puede escribir mediante simple
inspección, sin verificar la multiplicación que cumplen ciertas reglas fijas.
Su aplicación simplifica y sistematiza la resolución de muchas multiplicaciones
habituales.
Cada producto notable corresponde a una fórmula de
factorización. Por ejemplo, la factorización de una diferencia de cuadrados perfectos
es un producto de dos binomios conjugados, y recíprocamente.
Binomio de suma al cuadrado
Un binomio al cuadrado (suma) es igual es igual al cuadrado
del primer término, más el doble producto del primero por el segundo más el
cuadrado segundo.
(a + b)2 = a2 + 2 · a · b + b2
(x + 3)2 = x 2 + 2 · x ·3 + 3 2 = x 2 + 6 x + 9
Binomio de resta al cuadrado
Un binomio al cuadrado (resta) es igual es igual al cuadrado
del primer término, menos el doble producto del primero por el segundo, más el
cuadrado segundo.
(a − b)2 =
a2 − 2 · a · b + b2
(2x − 3)2 =
(2x)2 − 2 · 2x · 3 + 3 2 = 4x2 − 12 x + 9
Suma por diferencia
Una suma por diferencia es igual a diferencia de cuadrados.
(a + b) ·
(a − b) = a2 − b2
(2x + 5) ·
(2x - 5) = (2 x)2 − 52 = 4x2 − 25
Binomio al cubo
Binomio de suma al cubo
Un binomio al cubo (suma) es igual al cubo del primero, más
el triple del cuadrado del primero por el segundo, más el triple del primero
por el cuadrado del segundo, más el cubo del segundo.
(a + b)3 = a3 + 3 · a2 · b + 3 · a · b2 + b3
(x + 3)3 = x 3 + 3 · x2 · 3 + 3 · x· 32 + 33 =
= x 3 + 9x2 + 27x + 27
Binomio de resta al cubo
Un binomio al cubo (resta) es igual al cubo del primero,
menos el triple del cuadrado del primero por el segundo, más el triple del
primero por el cuadrado del segundo, menos el cubo del segundo.
(a − b)3 = a3 − 3 · a2 · b + 3 · a · b2 − b3
(2x - 3)3 = (2x)3 - 3 · (2x)2 ·3 + 3 · 2x· 32 - 33 =
= 8x 3 - 36 x2 + 54 x - 27
Trinomio al cuadrado
Un trinomio al cuadrado es igual al cuadrado del primero,
más el cuadrado del seguno, más el cuadrado del tercero, más el doble del
primero por el segundo, más el doble del primero por el tercero, más el doble
del segundo por el tercero.
(a + b +
c)2 = a2 + b2 + c2 + 2 · a · b + 2 · a · c + 2 · b · c
(x2 − x +
1)2 =
= (x2)2 +
(−x)2 + 12 +2 · x2 · (−x) + 2 x2 · 1 + 2 · (−x) · 1 =
= x4 + x2 + 1 − 2x3 + 2x2 − 2x =
= x4 − 2x3 + 3x2 − 2x + 1
Potencias y Radicales!!
La potenciación es una forma abreviada de escribir
multiplicación de factores iguales. La operación inversa es la radicación.
Abreviando la multiplicación y la división
La potenciación es el producto de varios factores iguales.
Para abreviar la escritura, se escribe el factor que se repite (base) y en la
parte superior derecha del mismo se coloca el número de veces que se multiplica
(exponente).
La radicación representa la operación inversa, siendo el
número dividido el radicando y el número por el que éste se divide, el índice.
Por ejemplo:
domingo, 23 de septiembre de 2012
Caso 1; Multiplicación Monomio por Monomio
en estas multiplicaciones es de vital importancia resolverlas en el siguiente orden; 1°signo, 2°coeficiente, 3° parte literal.
ademas saber que la multiplicación de cuantos sean monomio siempre dará monomio de resultado.
ademas saber que la multiplicación de cuantos sean monomio siempre dará monomio de resultado.
Multiplicación de Monomio y Polinomios !!
la multiplicación, consiste en sumar una cantidad o termino tantas beses como la otra cantidad lo indique.
pero antes de resolver una multiplicación ya sea con monomio o polinomio es necesario conocer sus propiedades de la multiplicación.
- conmutativa: nos dice que el orden de los factores no afecta el resultado.
- distributiva: nos dice que es lo mismo multiplicar la suma de 2 números por otro. que multiplicar cada uno de los números de la suma por el otro y luego sumarlo.
- asociativa: nos dice que el cambiar la asociación de factores del producto nos da el mismo resultado.
- elemento neutro: nos dice que todo numero multiplicado por uno, dará siempre como resultado el mismo numero.
- elemento inverso multiplicativo: nos dice que al multiplicar el inverso por el numero el resultado sera 1.
- absorbente: nos dice que todo numero multiplicado por 0 siempre sera igual a 0.
Así como también es importante tener en cuenta la:"ley de los signos" y "ley de los exponentes"
la multiplicación de términos algebraicos se pueden calcificar en 3 maneras:
- Multiplicación de monomio por monomio
- Multiplicación de monomio por polinomio
- Multiplicación de polinomio por polinomio
Operaciones Básicas con Polinomios!!
SUMA
Para sumar 2 o mas polinomios, se coloca los polinomios ordenados de manera vertical( uno por debajo del otro).
se ordena la ecuación de tal manera que todos los términos semejantes queden encimados para así lograr facilitar las operaciones.
RESTA
para realizar una resta de polinomio el procedimiento es prácticamente el mismo, lo único que se tiene que hacer escribir todos los signos de el sustraendo (esto debido a la multiplicación de signos). el minuendo se coloca tal cual
jueves, 20 de septiembre de 2012
Evaluación Numérica de Expresiones Algebraicas !
para llevar a cabo la evaluación de una exprecion algebraica, es necesario saber el valor de las incongnitas que pueda presentar (X,Y,Z......). para de esta manera sustituir las literales por sus valares correspondientes y así realizar las operaciones que se indiquen para encontrar el resultado.
Lenguaje Algebraico !!
para resolver un problema matemático utilizando el álgebra, es necesario traducir el problema de un lenguaje común a un lenguaje.
para esto, es necesario identificar expresiones comunes que permitan la traducción a un lenguaje algebraico y viceversa.
Signos de Agrupacion

la principal función de los signos de agrupación, es el indicar que las cantidades contenidas entre ello deben de considerarse como un "todo". se utilizan para afectar el orden de las operaciones y cuando existen estos signos dentro de una operación o incluso de otro(s) signo(s) estos se devén de resolver primero
Reducción de Términos Semejantes
los terminos son semejantes solo encaso de tener la(s) misma(s) literal(es) y mismos exponentes. en ser asi se, pueden reducir estos terminos sumando o restando solo los coeficientes y dejando la parte literal sin ningún cambio.
Grados de una Ecuación!
en un polinomio pueden llegar a existir 2 o mas términos semejantes, que son términos con el mismo literal y exponente, que al ser reducidos al máximo posible nos deja una ecuación algebraica mas sencilla de resolver.
una vez que se tiene una ecuación mas sencilla de resolver, se puede definir los grados absolutos y relativos ya sea de cada termino por separado o de el polinomio en general.
"Grado absoluto"
el grado absoluto d e un termino o ecuación, es la suma de todos los exponentes de sus literales y se escribe te manera general. en el caso de ser de una ecuación, se anota la suma de los exponentes del termino mas grande.
"Grado relativo"
se conoce como grado relativo a cada uno de los exponentes de un termino de manera individual, por lo cual no se suman, se anotan tal cual con su correspondiente literal.
Clasificación de Expresiones Algebraic
de acuerdo con el numero de términos algebraicos que contenga una exprecion, se pueden calcificar en 2 tipos:
"Monomio"
es un exprecion algebraica formada por un solo termino:
"Polinomio"
es una exprecion algebraica que indica la suma o resta de 2 o mas términos (pueden ser semejantes o no)
A su vez en polinomio puede dividirse en:
binomio; polinomio formado por 2 términos.
-3x + 5xy
trinomio;polinomio que consta de 3 terminos.
6y - 2zq + 8a
Expresiones Algebraicas
una exprecion algebraica es la combinacion de: signo, coeficiente, literal, exponente.
TERMINO ALGEBRAICO:
es una exprecion formada por números y literales, no separadas entre si por signos como "+ -" los elemtos que conforman un termino algebraico son 4:- COEFICIENTE: son los numeros que aparecen multiplicando a las literales.
- SIGNO: indica si un termino es negativo o positivo.
- LITERAL: esta formado por letra que aparecen en el termino con sus correspondientes exponentes.
- EXPONENTE. indica el numero de beses que se utiliza un termino como factor para multiplicarse a si mismo.
Operaciones Básicas del Álgebra
Suma ( + ) : si los sumados tiene el mismo signo, se suma y prevalece el signos de ambos.
A+B=C
(donde A y B son los sumados y C es el suma)
Resta ( - ) : si los signos son iguales se suman y prevalece el signo de ambos y si se tienen signos diferentes, al numero mayor se le resta el menor y prevalece el signo del mayor.
A-B=C
(donde A es minuendo, B es sustraendo y C diferencia)
Multiplicación ( X( ) . ) : es el numero de beses que un factor se debe de sumar por si mismo tantas beses como el otro factor indique.
A:B=C
(donde A y B son factores y C producto)
Divicion ( 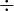
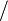
 ) : consiste en conocer el numero de beses que cabe un numero dentro de otro.
) : consiste en conocer el numero de beses que cabe un numero dentro de otro.
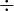
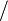
 ) : consiste en conocer el numero de beses que cabe un numero dentro de otro.
) : consiste en conocer el numero de beses que cabe un numero dentro de otro.
d/D=A
(donde d es divisor. D es dividendo y A cociente)
Potenciacion ( n ) : es la multiplicacion de un factor llamado "base" tantas bese como su exponente lo indique.
A^n
(donde A es la base y n es el exponente)
Clasificación de los Números
los números, se calcifican principalmente en 4 grupos los cuales son:
 Naturales ( N ) : se resumen como cualquier numero del 1 al infinito, que se pueden usar para contabilizar elementos y/o cosas.
Naturales ( N ) : se resumen como cualquier numero del 1 al infinito, que se pueden usar para contabilizar elementos y/o cosas.
Enteros ( Z ) : los números enteros abarcan del infinito (negativo) al infinito (positivo), y se resumen como los numeros naturales y sus opuestos.
Racionales ( Q ) : es todo numero aquel que se puede mostrar como fracción o decimal exacta.
Irracionales ( I ) : es todo numero aquel que no puede mostrarse como decimal exacto y/o fracciones no pertenecientes a los números enteros.
Reales ( R ) : son todos los números.
Enteros ( Z ) : los números enteros abarcan del infinito (negativo) al infinito (positivo), y se resumen como los numeros naturales y sus opuestos.
Racionales ( Q ) : es todo numero aquel que se puede mostrar como fracción o decimal exacta.
Irracionales ( I ) : es todo numero aquel que no puede mostrarse como decimal exacto y/o fracciones no pertenecientes a los números enteros.
Reales ( R ) : son todos los números.
La Historia Del "Álgebra"
los origenes del algebra se remontan a los antiguos babilonios. quienes hubiesen inventado un sofisticado sistema aritmetico, con el cual se realizaron los primeros calculos de manera algebraica.
Pero no fue asta que con el apoyo de la geometria griega y matematicos chinos, que se lograron sentar la bases del algebra como tal, entre las cuales destacan. -la generacional de las formulas. -el desarrollo del sistema para exponer y resolver ecuaciones. Años despues, esta tematico fue retomada y mejorada por pensadores de la antigua "alejandrina" quienes plasmaron sus conocimientos en el libro "arithmetica de Diophantus", que posteriormente con la ayuda de los musulmanes y de Diofantos sentaron las bases para que "al-khwarizmi resolviera una serie de ecuaciones con métodos generales.
 los origenes de la palabra algebra dan con la palabra Al-jarb, nombre de un libro escrito por el musulman islamico "muhammad" conocido como el padre del algebra.
los origenes de la palabra algebra dan con la palabra Al-jarb, nombre de un libro escrito por el musulman islamico "muhammad" conocido como el padre del algebra.
Pero no fue asta que con el apoyo de la geometria griega y matematicos chinos, que se lograron sentar la bases del algebra como tal, entre las cuales destacan. -la generacional de las formulas. -el desarrollo del sistema para exponer y resolver ecuaciones. Años despues, esta tematico fue retomada y mejorada por pensadores de la antigua "alejandrina" quienes plasmaron sus conocimientos en el libro "arithmetica de Diophantus", que posteriormente con la ayuda de los musulmanes y de Diofantos sentaron las bases para que "al-khwarizmi resolviera una serie de ecuaciones con métodos generales.
Suscribirse a:
Comentarios (Atom)


